گاه برای ساختنباید ویران کرد
گاه برای داشتنباید گذشت
گاه در اوج تمناباید نخواست
گاه برای داشتنباید گذشت
گاه در اوج تمناباید نخواست

|
| ابریق می مرا شکستی، ربی | بر من در عیش را ببستی، ربی | |
| من مِی خورم و تو می*کنی بدمستی | خاکم به دهن مگر که مستی، ربی |
| ناکرده گنه در این جهان کیست بگو! | آن کس که گنه نکرد چون زیست بگو! | |
| من بد کنم و تو بد مکافات دهی | پس فرق میان من و تو چیست بگو! |
| « | خیام اول کسی است که به تحقیق منظم علمی در معادلات درجات اول و دوم و سوم پرداخته، و طبقه*بندی تحسین*آوری از این معادلات آورده*است، و در حل تمام صور معادلات درجه سوم منظماً تحقیق کرده، و به حل (در اغلب موارد ناقص) هندسی آنها توفیق یافته، و رساله وی در علم جبر، که مشتمل بر این تحقیقات است، معرف یک فکر منظم علمی است؛ و این رساله یکی از برجسته*ترین آثار قرون وسطائی و احتمالاً برجسته*ترین آنها در این علم است. یکی دیگر از آثار ریاضی خیام رسالة فی شرح ما اشکل من مصادرات اقلیدس است. او در این کتاب اصل موضوعهٔ پنجم اقلیدس را دربارهٔ قضیهٔ خطوط متوازی که شالودهٔ هندسهٔ اقلیدسی است، مورد مطالعه قرار داد و اصل پنجم را اثبات کرد.[۳۰] به نظر می*رسد که تنها نسخه کامل باقیمانده از این کتاب در کتابخانه لایدن در هلند قرار دارد.[۳۱] «در نیمهٔ اول سدهٔ هیجدهم، ساکری اساس نظریهٔ خود را دربارهٔ خطوط موازی بر مطالعهٔ همان چهارضلعی دوقائمهٔ متساوی*الساقین که خیام فرض کرده بود قرار می*دهد و کوشش می*کند که فرضهای حاده و منفرجه*بودن دو زاویهٔ دیگر را رد کند.»[۳۲] درکتاب دیگری از خیام که اهمیت ویژه*ای در تاریخ ریاضیات دارد رسالهٔ مشکلات الحساب (مسائلی در حساب) هرچند این رساله هرگز پیدا نشد اما خیام خود به این کتاب اشاره کرده*است و ادعا می*کند قواعدی برای بسط دوجمله*ای  کشف کرده و اثبات ادعایش به روش جبری در این کتاب است. بنابرین از دیگر دست*آوردهای وی موفقیت در تعیین ضرایب بسط دو جمله*ای (بینوم نیوتن) است که البته تا سده قبل نامکشوف مانده بود و به احترام سبقت وی بر اسحاق نیوتن در این زمینه در بسیاری از کتب دانشگاهی و مرجع این دو جمله*ای*ها «دو جمله*ای خیام-نیوتن» نامیده می*شوند. نوشتن این ضرایب به صورت منظم مثلث خیام-پاسکال را شکل می*دهد که بیانگر رابطه ای بین این ضرایب است. کشف کرده و اثبات ادعایش به روش جبری در این کتاب است. بنابرین از دیگر دست*آوردهای وی موفقیت در تعیین ضرایب بسط دو جمله*ای (بینوم نیوتن) است که البته تا سده قبل نامکشوف مانده بود و به احترام سبقت وی بر اسحاق نیوتن در این زمینه در بسیاری از کتب دانشگاهی و مرجع این دو جمله*ای*ها «دو جمله*ای خیام-نیوتن» نامیده می*شوند. نوشتن این ضرایب به صورت منظم مثلث خیام-پاسکال را شکل می*دهد که بیانگر رابطه ای بین این ضرایب است.به هر حال قواعد این بسط تا 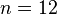 توسط طوسی (که بیشترین تأثیر را از خیام گرفته) در کتاب «جوامع الحساب» آورده شده*است.روش خیام در به دست آوردن ضرایب منجر به نام گذاری مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی زبان*ها آن را به نام مثلث پاسکال می*شناسند که البته خدشه*ای بر پیشگامی خیام در کشف روشی جبری برای این ضرایب نیست. توسط طوسی (که بیشترین تأثیر را از خیام گرفته) در کتاب «جوامع الحساب» آورده شده*است.روش خیام در به دست آوردن ضرایب منجر به نام گذاری مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی زبان*ها آن را به نام مثلث پاسکال می*شناسند که البته خدشه*ای بر پیشگامی خیام در کشف روشی جبری برای این ضرایب نیست. |
» |
 کشف کرده و اثبات ادعایش به روش جبری در این کتاب است. بنابرین از دیگر دست*آوردهای وی موفقیت در تعیین ضرایب بسط دو جمله*ای (بینوم نیوتن) است که البته تا سده قبل نامکشوف مانده بود و به احترام سبقت وی بر اسحاق نیوتن در این زمینه در بسیاری از کتب دانشگاهی و مرجع این دو جمله*ای*ها «دو جمله*ای خیام-نیوتن» نامیده می*شوند. نوشتن این ضرایب به صورت منظم مثلث خیام-پاسکال را شکل می*دهد که بیانگر رابطه ای بین این ضرایب است.
کشف کرده و اثبات ادعایش به روش جبری در این کتاب است. بنابرین از دیگر دست*آوردهای وی موفقیت در تعیین ضرایب بسط دو جمله*ای (بینوم نیوتن) است که البته تا سده قبل نامکشوف مانده بود و به احترام سبقت وی بر اسحاق نیوتن در این زمینه در بسیاری از کتب دانشگاهی و مرجع این دو جمله*ای*ها «دو جمله*ای خیام-نیوتن» نامیده می*شوند. نوشتن این ضرایب به صورت منظم مثلث خیام-پاسکال را شکل می*دهد که بیانگر رابطه ای بین این ضرایب است.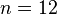 توسط طوسی (که بیشترین تأثیر را از خیام گرفته) در کتاب «جوامع الحساب» آورده شده*است. روش خیام در به دست آوردن ضرایب منجر به نام گذاری مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی زبان*ها آن را به نام مثلث پاسکال می*شناسند که البته خدشه*ای بر پیشگامی خیام در کشف روشی جبری برای این ضرایب نیست.
توسط طوسی (که بیشترین تأثیر را از خیام گرفته) در کتاب «جوامع الحساب» آورده شده*است. روش خیام در به دست آوردن ضرایب منجر به نام گذاری مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی زبان*ها آن را به نام مثلث پاسکال می*شناسند که البته خدشه*ای بر پیشگامی خیام در کشف روشی جبری برای این ضرایب نیست.
| برخیز و بیا بتا برای دل ما | حل کن به جمال خویشتن مشکل ما | |
| یک کوزه شراب تا بهم نوش کنیم | زان پیش که کوزه*ها کنند از گل ما |
| چون عهده نمی*شود کسی فردا را | حالی خوش کن تو این دل شیدا را | |
| می نوش بماهتاب ای ماه که ماه | بسیار بتابد و نیابد ما را |
| قرآن که مهین کلام خوانند آن را | گه گاه نه بر دوام خوانند آن را | |
| بر گرد پیاله آیتی هست مقیم | کاندر همه جا مدام خوانند آن را |
| گر می نخوری طعنه مزن مستانرا | بنیاد مکن تو حیله و دستانرا | |
| تو غره بدان مشو که می مینخوری | صد لقمه خوری که می غلام*ست آنرا |
| عمرت تا کی به خودپرستی گذرد | یا در پی نیستی و هستی گذرد | |
| می نوش که عمریکه اجل در پی اوست | آن به که به خواب یا به مستی گذرد |
| کس مشکل اسرار اجل را نگشاد | کس یک قدم از دایره بیرون ننهاد | |
| من می*نگرم ز مبتدی تا استاد | عجز است به دست هر که از مادر زاد |
| کم کن طمع از جهان و میزی خرسند | از نیک و بد زمانه بگسل پیوند | |
| می در کف و زلف دلبری گیر که زود | هم بگذرد و نماند این روزی چند |
| گرچه غم و رنج من درازی دارد | عیش و طرب تو سرفرازی دارد | |
| بر هر دو مکن تکیه که دوران فلک | در پرده هزار گونه بازی دارد |
نظر