جدول اعداد مارپیچ گن Gann Square of Nine

[Navid]

ادامه تحقيقات مقدماتي - جدول اعداد مارپيچي گن

اگر در جدول زير ، اعداد مارپيچي مشاهده کنيد شکل پست قبلي ديده مي شود
بدين گونه که :

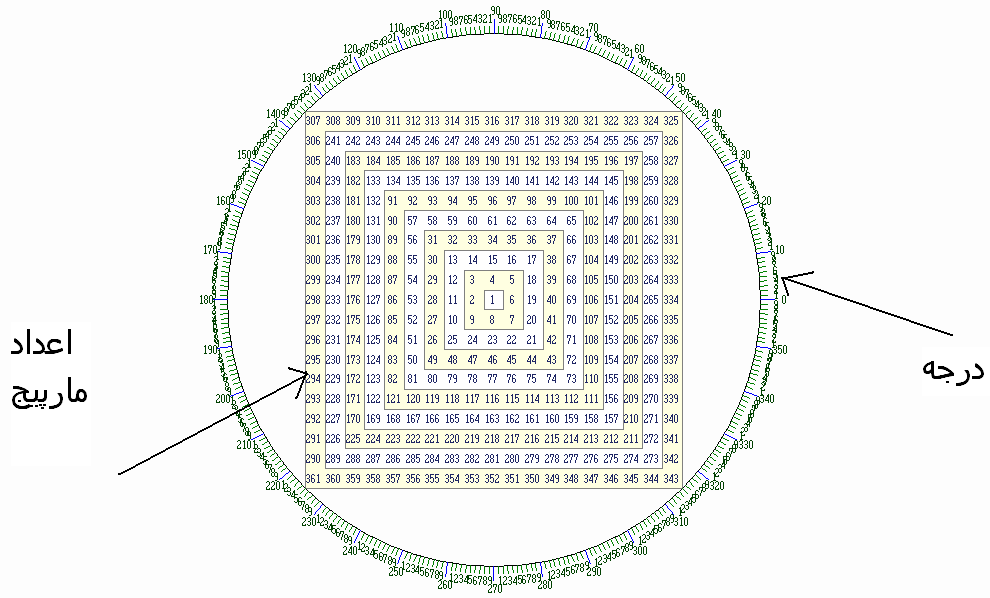
اگر شما جمع دو عدد4 و 8 رابر دو تقسيم کنيد عدد 6 ميشود.
و به همين روال ادامه دهيد.
(4+8)/2 = 6
(14+24)/2 = 19
(32+48)/2 = 40
و اگر اين سه عدد را به هم وصل کنيد ( براي مثال 4و 8 و 6) همان شکل به خوبي ديده مي شود.

اين عمل را در چند جهت امتحان گرديد و ديده شد در تمام جهت ها اين شکل ديده مي شود.

تعميم بحث : به دليل آنکه اگر از (4،8،6) اگر رسم کنيم هيچ وقت به عدد 144 نمي رسيد. پس احتمال داشته دهنه باز شدن آن را به دليل رخداد ها و عوامل مختلف به جولو و عقب حرکت داده شده است.

احتمال مي دهم براي به دست آوردن آنکه چرخه هاي جدول مارپيچي را تا عددي ادامه داد که اين خط ( خط گفته شده در بالا ) در نقطه 144 درجه دايره را قطع کند. ( البته با توجه به مطالبي که در قسمت تعميم بحث گفته شد.) بايد رخداد هاي طبيعي آن زمان و اعداد و ارقام (همانند روز سال کبيسه ، سال شمسي ، سال قمري ، سال ميلادي ، ساعت ، فاصله از گرينويچ ، فاصله از استوا وغيره ) بررسي کرد.

با تشکر محمد نبي زماني

[Saeed_Yousefi]

با سلام
بدلیل کمبود وقت از دوستان خواهش میکنم که الباقی مطالب را از پی دی اف بخونن و یا یکی از دوستان زحمت انتقال مطالب فایل به اینجا را بکشه.
حق نگهدارتان

[Navid]

فرض و نتايج آنها

دوستان من يک کار کوچيک تقريبا انجام دادم
3 تا فرض اصلي انجام دادم و بقيه زير فرض
يکي از فرض اصلي اين بوده => فيبوناچي و گن

نميدونم دوستان فيبوناچي بازار ميشناسند يا علمي براي همين توضيح مختصر ميدهم.
فيبوناچي يک رياضي دان بود ، دنباله تعريف کرده که به سمت بي نهايت واگراست(دنباله هاي را سري نيز ميگويند.)
کليه دنباله ها خاصيتهاي توابع را دارند ( هر چند مثل توابع پيوسته نيستند.)
سري فيبوناچي جواب خيلي از سوالات علمي را داده است و توانسته خيلي از نسبتهاي خلقت را کشف کند
سري فيبوناچي از يک سري اعداد تشکيل شده است که با تقسيم آنها بر روي هم نسبتي به دست مي ايد که اين نسبت از اهميت بالاي برخوردار است.
بر اساس تاريخ تولد آن فکر نميکنم فيبوناچي بازار ارز را به خود ديده باشد.( حتي مشابه آن در زمان خودش)
کارشناسان و متخصصان بازار از اين نسبتهاي فيبوناچي استفاده کرده و طبق تعاريفي که رياضي دانها از اين دنباله داشتند و اشکال به دست اورده بودند استفاده کردند و در بازار ارز استفاده کرده اند.

زير فرض 1 احتمال دارد گن از فيبوناچي استفاده کرده باشد.
فيبوناچي رابطه خود را در زمان قبلتر از گن گفته است در نتيجه روابط فيبوناچي در اختيار آقاي گن بوده پس احتمال ميرود او از اين رابطه استفاده کرده باشد.

براي اين منظور جدول مارپيچگن را رسم کرده و اعداد روي ان را بر اساس فيبوناچي مارک دار کرديم. نتيجه که به دست آمد مشابه نتيجه گن بود (زاويه 144 با کمي تقريب)

اين زاويه خصوصيتي که دارد نسبت به 135 و 180 نسبت 1/2 را دارد و عدد شاخص آن9 است.

فرض دوم در دنيا تقارن به کرات ديده ميشود .

نمونه
زن مرد- زمين آسمان - ماه و خورشيد-و غيره

پس احتمال دارد دارد عدد 216تقارن عدد 144 است و اين مورد جواب داد.

با احترام
محمد نبي زماني

[sarababa]

با عرض سلام وصبح بخیر

دوستان باید بدونیم که اقای گن به دوره های زمانی بسیار بسیا راهمیت میداده مثلا به 2 تا 7 ژانویه و 15 تا 21 ژانویه اگر به این دورهای زمانی خوب دقت کنید خواهید دید که سقف وکفهایی که در این دوره ها ساخته میشود تا زمانی که این سقف و کفها درهم نشکند روند ادامه خواهد یافت

[SAMADALDIN]

درود

خدا قوت...
بنده نگاهی گذرا به جزوه شما داشتم. خیلی خوب بود از شما تشکر میکنم. البته تصمیم گرفتم امشب کامل مطاله کنم.

آموزش را به جاهایی رسانده اید. که خوب است. اگر در حوصله تان است ادامه دهید. بیشتر کاربران مطاله از روی فروم را ترجیح میدهند به استفاده از جزو... آن هم برای این است که کم کم مطلب درج میشود. ولی استفاده از جزو زمان بر است و چشم را خسته میکند.

نمونه ای از تحلیل های خود را قرار دهید. بنده نرم افزاری را در این پست معرفی کردم. باشد که کمکتان کند...

[SAMADALDIN]

درود...

خدا قوت....

همان طور که گفتم دیشب جزو شما را کامل مطالعه کردم. کامل بود. بابت زحمتی که کشیدید تشکر میکنم. بنده آن قسمت که مربوط به محاسبات بود را در کتاب اصلی نخوندم. حوصله اش نبود. رفتم سر مطالب اصلی. چون نرم افزارها کارهای محاسباتی را انجام میدهند. در ترجمه شما آن مطالب را خواندم و جالب بود.

یک نسخه از آن را در کتابخانه فارسی گن قرار میدهم.

زمانی را بگذارید و نمونه هایی را درج بفرمایید. بنده هم کمی سر خلوت بشود جند فرمول در اکسل نوشته بودم برای سهولت کار خودم. میگردم پیدا میکنم. و با مطالبی که از محاسبات جزو شما آموختم. پیرایش میکنم. و براتون قرار میدهم....

[Arash72]

با سلام.
من هم جزوه رو کامل خوندم.خیلی خوب بود.در بازار ایران هم در مورد دو سهم سپاها و ثشاهد که روندشون رو دنبال میکنم تستش کردم و نتایج جالبی داشت که حتما در پست های بعدی راجع به اون صحبت میکنم.

تقریبا جزوه رو کامل فهمیدم.اگر کسی از دوستان مشکلی داشت مطرح کنه.ان شا الله بتونم کمک کنم.

[SAMADALDIN]

درود...

برای اینکه موضوع نشر آموزش از روی جزو توسط جناب یوسفی تکمیل نشده بود.

تحلیلها و مطالب مربوط به این تاپیک منتقل شد.

تا جناب یوسفی فرصت کنند و آموزش را تکمیل کنند...

[Saeed_Yousefi]

درود
آقای گن خطوطی را از وسط جدول به دایره بیرونی رسم میکرد. این خطوط در بسیاری از روشهای تحلیل در کار با جدول کاربرد دارد.
گن این خطوط را زاویه یا انگل Angle نامگذاری کرد. زاویه ها یا انگلها با درجه ای که روی دایره لمس میکنند تعیین مشوند ( نامیده میشوند).
برای مثال در شکل زیر زاویه 70 درجه از وسط جدول به درجه 70 روی دایره رسم شده.
همچنین شاهد رسم زاویه 200 درجه هستیم.
هر چند این نوع تعیین ازاویه با مفهوم زاویه مرسوم در هندسه فرق دارد اما چون آقای گن این خطوط را زاویه نامید ما در اینجا نیز از اصطلاحات او استفاده میکینم.



گن همیشه جدول را با دایره بیرونی استفاده نمیکرد . چون دایره بیرونی جدول کار را خیلی بزرگ میکنه.
در شکل زیر جدول بدون دایره ای میبینید که گن از اون استفاده میکرده. خود جدول هر 45 درجه درجه بندی شده:

در شکل زیر نقاط A , B , C روی جدول مشاهده میکنید به غیر از نقطه A بعضا گن درجه 0 را روی نقاط B و Cنیز قرار میداده که ما در اینجا فقط با نقطه A کار داریم.



روکش یا اورلی overlay

درود
کلا دو نوع روکش یا اورلی overlay وجود بنامهای : روکش زاویه ای و روکش اشکال هندسی.
در شکل زیر زوایای کراس مورب و کراس عادی ( cardinal and diagonal crosses ) را میببینید که زوایای ثابت روی سطح جدول هستند. اما میشه این زوایا را روی یک پلاستیک شفاف کشید و یک روکش درست کرد .
روکش پلاستسکی روی جدول قرار میگیره و به راحتی میتونیم اونو بچرخونیم . زوایای این روکش با فاصله 45 درجه از هم دیگه قرار دارند و میتونیم روی هر عددی قرار بدیم و نقطه شروه محاسبه را از اون نقطه بگیریم و زوایای مربوط به اون عدد را مشاهده کنیم.
به عبارت دیگر یک کراس مورب و عادی متحرک را خواهیم داشت.

زاویه 0 درجه روکش همیشه با خطی ضخیمتر از بقیه زوایا مشخص میشود.
نامگذاری ( تشخیص ) بقیه زوایا با فاصله ای که از 0 درجه دارند صورت میگیره:
زاویه روبرویی 0 درجه روکش 180 درجه نامیده میشه.
2 زاویه ای که به میزان 45 درجه از خط 0 درجه در دو طرف قرار دارند روکشهای 45 درجه و 315 درجه نامیده میشوند.
2 زاویه ای که از دو طرف 0 درجه 90 درجه فاصله دارند را روکش 90 درجه و 270 درجه مینامند.
و 2 زاویه بعدی نیز 135 و 225 نامیده میشوند.

روکشهای با تقسیم بندی 45 درجه همیشه توسط گن استفاده نمیشد . در زیر نمونه ای از روکش با تقسیم بندی 60 درجه را میبینید:


نوع خاصی از روکش را میبینید که گن از اون نیز استفاده میکرده با زوایای 180 درجه و 2 زاویه دیگه که هر دو 144 درجه از هر طرف از 0 درجه فاصله دارند که با 144 درجه و 216 درجه مشخص شده اند:

[Saeed_Yousefi]

روکشهای اشکال هندسی


نوع دوم روکش روکشهای اشکال هندسی هستند که آقای گن از اشکال مثلث و مربع به عنوان روکش استفاده میکرد.
در شکل زیر روکش نوع مثلث را میببینید :

در هر شکل 2 نوع خط استفاده میشود : خطوطی که خود شکل هندسی را تشکیل میده ( اضلاع ) که با خط ضخیم و تیره رسم میشه و نوع دوم خطوطی که از گوشه های شکل به وسط جدول رسم میشه که خطوط کم رنگ و نازکی هستند.

و در این شکل نیز روکش نوع مربع را میبینید . اضلاع خطوط پر رنگ و خطوط داخلی اضلاع کم رنگ هستند:

[Saeed_Yousefi]

2 روش برای تنظیم روکش روی جدول

دو روش برای تنظیم روکش روی جدول وجود داره روش اول به این صورت که زاویه 0 روکش را روی یکی از درجه های دایره بیرونی جدول قرار بدیم.
در شکل میبینیم که زاویه 0 روکش روی درجه 212 دایره بیرونی قرار گرفته و میتونیم اعداد جدول را که روی زوایای روکش قرار دارند را ببینیم:
برای مثال :
زاویه 0 درجه اعداد 123 و 83و 50 و 51 و 26 جدول را در بر گرفته .
و زاویه 90 درجه اعداد 159 و 113 و 75 و 74 و 44 و 22 جدول را در بر گرفته.
و زاویه 315 درجه اعداد 128 و 87 و 54 و 29 و 11 و 12 را در بر گفته .
و الباقی زوایا نیز . . . . . .

و این موضوع معنی اینکه روکش خودش یک نوع کراس مورب و عادی متحرک هست را روشن تر میکنه.

روش دومی که میشه روکش را تنظیم کرد اینه که زاویه 0 روکش را روی یکی از اعداد جدول قرار بدیم:
در شکل زیر عدد 0 روکش روی خانه عدد 154 تنظیم شده.
وقتی روکش روی یکی از خانه های جدول تنظیم میشه باید دقت داشته باشید که خط زاویه روکش دقیقا از وسط اون خانه بگذره.

درود
وقتی از روکشهای اشکال هندسی استفاده میکنیم هر دو روشی را که روکش زاویه دار مشخص میکرد را در بر میگیره.
در شکل زیر یکی از گوشه های مثلث روی 20 درجه دایره قرار گرفته ( روش اول ) و خط داخلی مثلث نیز از وسط خانه 164 گذشته( روش دوم ):



طریقه صحیح قرار دادن روکش روی اعداد جدول

درود
قیمتهای سهام همیشه اعداد صحیح نیستند . مثلا قیمت 73.25 را چطور میتونیم روی جدول مشخص کنیم؟
در شکل زیر خونه های جدول به اندازه 0.25 تقسیم بندی شده اند. میبینید که شماره هر خانه جدول دقیقا در وسط جدول قرار دارند. مشاهده میکنیم که خط زاویه 45 درجه دقیقا از وسط هر خونه میگذره.
اگه قرار باشه کراسهای مورب و کراسهای عادی( + و X ) را با خط مشخص کنیم . این خطوط میبایست هر خانه از جدول از وسط نصف کنند.
همانطور که مشاهده میکنید عدد 35 در وسط خانه 35 و عدد 36 در وسط خانه 36 قرار دارد اگر از خانه 35 به خانه 36 حرکت کنیم میبینیم که عدد 35.5 روی خط فی مابین دو خانه قرار داره.
مشکلی که در هنگام تنظیم روکش روی اعداد وجود داره موقعی بوجود میاد که عددی با اعشار بیشتر ار پنج دهم (0.5) داشته باشیم. مثلا عدد 34.75 در خانه 35 و عدد 35.75 در خانه 36 قرار دارد و الی آخر . . . . اگر قرار باشد که روکش را روی عدد 39.75 قرار دهیم در واقع خط روکش از قسمت بالایی خانه 40 خواهد گذشت.

در شکل زیر برخی اعداد از وسط جدول ( وسط خانه شماره 1 ) به بعضی نقاط با زاویه ای رسم شده :
اولین خط از وسط جدول رسم شده به قیمت 34.5 این خط با درجه 80.78 تلاقی خواهد کرد که از مستقیما از وسط خانه 34 و 35 میگذره.
دومین خط از وسط جدول رسم شده به قیمت 36.25 این خط با درجه 53.48 تلاقی خواهد کرد که از قسمت راست خانه 36 میگذره.
سومین خط از وسط جدول رسم شده به قیمت 39 این خط با درجه 18.43 تلاقی خواهد کرد که دقیقا از وسط خانه 39 میگذره.
خط چهارم از وسط جدول رسم شده به قیمت 39.75 این خط با درجه 4.61 تلاقی خواهد کرد که از نیمه بالایی خانه 40 میگذره.

[Saeed_Yousefi]

درجه های زوایای هر خانه از جدول

مشاهده کردیم وقتی که خطی که از وسط جدول به عدد 39 جدول وصل کنیم مقدار زاویه آن 18.43 درجه خواهد شد .
درجه زوایایی که از وسط جدول به اعداد سطح جدول رسم میشوند از طریق علم مثلثات قابل اندازه گیری میباشد. تمامی روابط ریاضی بین روکشها و اعداد سطح جدول از طریق علم مثلثات قابل محاسبه است.
اختصاص دادن یک بخش به عنوان مثلثات و قوانین ان از حوصله این کتاب خارج است بنا بر این درجه های خانه های ( اعداد ) جدول تا خانه 360 را لیست کردیم که در زیر میبینید:

[Saeed_Yousefi]

قوانین مربوط به جدول و درجه و روکش و . . . . کتاب تمام شد و کم کم میریم سراغ روشهای پیشبینی بازار طبق کتاب و معرفی استراتژی های پیش بینی بر اساس آنچه اموختیم.

[Saeed_Yousefi]

چارت میله ای

در این کتاب از چارت میله ای استفاده خواهد شد.

[Saeed_Yousefi]

توی چارت ساپورت رزیستنس و منطقه رنج و پایوت نشان داده شده.
پایوت ( در اینجا ) به نقطه ای گفته میشود که قیمت از آنجا ریورس میکنه! کندل یا میله ای که ریورس در اون صورت میگیره و پایوت بار pivot bar و های ( یا لوی) اون کندل یا میله را پایوت پرایسpivot price نامیده میشه! pivot price و pivot bar با همدیگه پایوت پوینت را تشکیل میدن! ( خلاصه اینجوری نوشته توکتاب دیگه )